堆和优先队列

发表于 | 更新于 | 分类于

堆和优先队列介绍

堆和优先队列是一种处理对数据集进行频繁的插入和删除操作时，往往需要快速确定最大或最小的元素这一问题的有效方法。

堆

它是一种树形组织，使我们能够迅速确定包含最大值的结点。维持一棵树的代价低于维持一个有序数据集的代价。同样，我们可以通过堆快速地找到包含最小值的元素。

优先队列

它是一个从堆自然衍生而来的数据结构。在优先队列中，数据保存在一个堆中，这样我们能够迅速确定下一个最高优先级的结点。所谓元素的“优先级”在不同的问题中意义也不相同。

堆和优先队列的一些应用

排序

具体来说，就是指堆排序。在堆排序中，要排序的数据首先存储在一个堆中。从堆中一次取出一个结点，放置到有序数据集的尾部。当取出每个结点时，它的下一个结点就会浮现到堆的顶部。堆排序与快速排序有相同的时间复杂度，但是在实际中，快速排序往往比堆排序复杂度略低，两者相差一个常量因子。

任务调度

任务调度会告诉操作系统接下来哪个进程将在CPU上运行。操作系统会不断调整进程的优先级。用优先队列来存储进程是相对比较高效的方法，因为它可以确保下一个将在CPU中运行的进程的优先级是最高的。

包裹分拣

快速公司通常用包裹分拣法来确定包裹递送的优先级。当扫描包裹时，高优先级的包裹将作为急快件投递出去。而非急快件将作为较低优先级的包裹投递出去。计算机系统通常使用优先队列来保证最高优先级的包在系统中运行最顺畅，因为这种方法十分高效。

霍夫曼编码

这是一种数据压缩方法，它使用霍夫曼树为数据符号分配编码。向出现频率较高的符号分配较短的编码，向出现频率较低的符号分配较长的编码。霍夫曼树是由较小的二叉树两两合并构成。由于每次都必须合并键值最小的二叉树，因此每次合并的两棵树都是从一个优先队列中取出的。

负载均衡

它用来维护管理一系列处理类似任务的服务。当连接请求到达时，优先队列可以确定哪个服务器能够最好地处理到达的任务。

堆

堆是一棵二叉树，通常其子结点存储的值比父结点的值小。所以，根结点是树中最大的结点。同样，我们也可以让堆向另一种方向发展，即每个子结点存储的值比父结点的值大。这样根结点就是树中最小的结点。这样的二叉树是局部有序的，任何一个结点与其兄弟结点之间都没有必然的顺序关系，但它与其父子结点有大小顺序关系。子结点比父结点小的堆称为最大值堆，这是因为根结点存储该树所有结点的最大值。反之，子结点比父结点大的堆称为最小值堆。

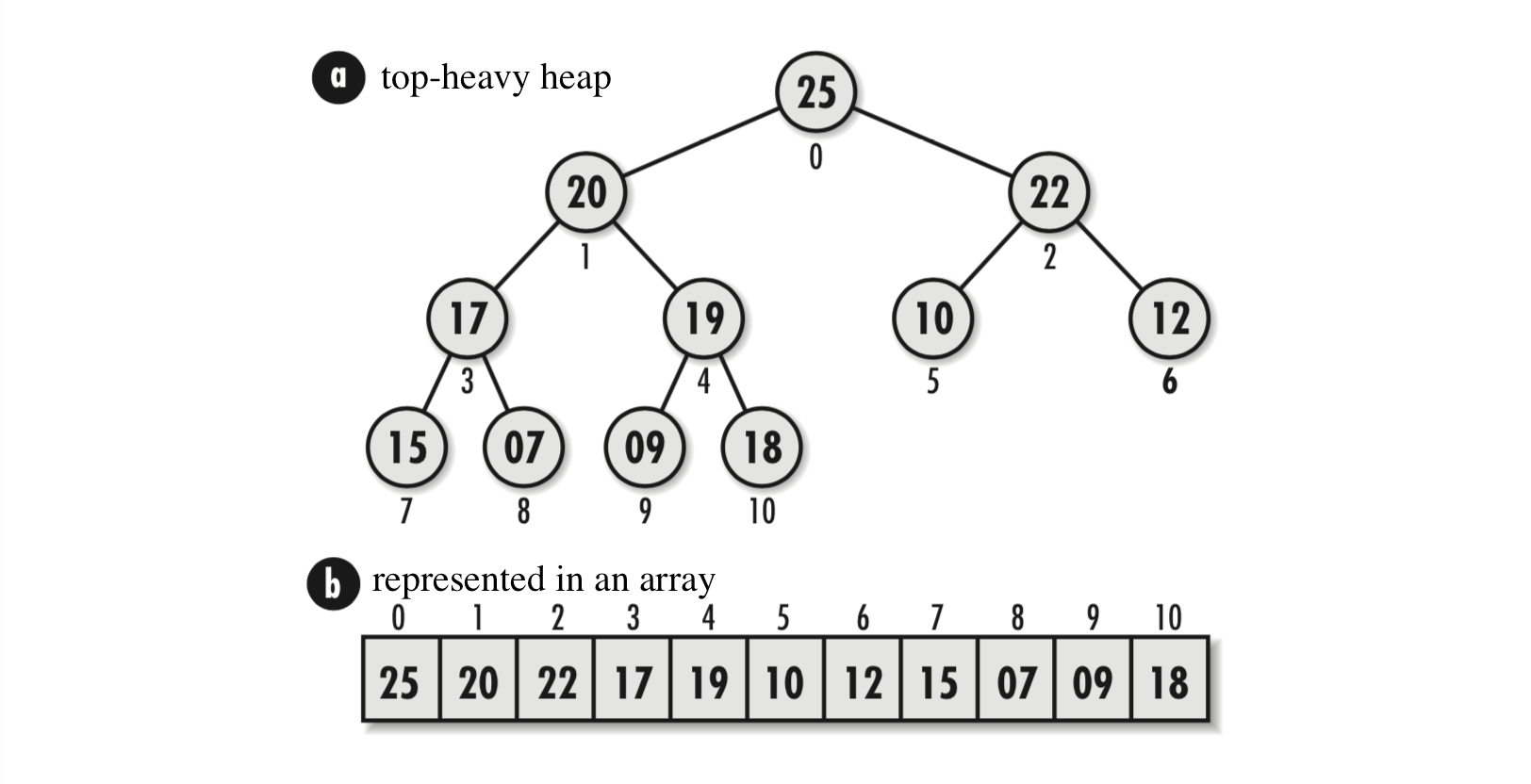
堆是左平衡的树（见第9章），所以随着结点的增加，树会逐级从左至右增长。因此对于堆来说，一个比较好的表示左平衡二叉树的方式是，将结点通过水平遍历的方式连续存储到一个数组中。假设有一个零索引数组（索引从零开始），这表示数组中处于位置 i 处的节点，其父结点位于 (i-1)/2 处，计算中要忽略 (i-1)/2 的小数部分。其左结点和右结点分别位于 2i+1 和 2i+2 位置上。这样的组织结构对于堆来说非常重要，因为通过它我们能迅速地定位堆的最后一个结点：最后一个结点指处于树中最深层最右端的结点。这在实现某些堆操作时非常重要。

堆的头文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*****************************************************************************
*                                                                            *
*  -------------------------------- heap.h --------------------------------  *
*                                                                            *
*****************************************************************************/

#ifndef HEAP_H
#define HEAP_H

/*****************************************************************************
*                                                                            *
*  Define a structure for heaps.                                             *
*                                                                            *
*****************************************************************************/

typedef struct Heap_ {

int                size;

int                (*compare)(const void *key1, const void *key2);
void               (*destroy)(void *data);

void               **tree;

} Heap;

/*****************************************************************************
*                                                                            *
*  --------------------------- Public Interface ---------------------------  *
*                                                                            *
*****************************************************************************/

void heap_init(Heap *heap, int (*compare)(const void *key1, const void *key2),
   void (*destroy)(void *data));

void heap_destroy(Heap *heap);

int heap_insert(Heap *heap, const void *data);

int heap_extract(Heap *heap, void **data);

#define heap_size(heap) ((heap)->size)

#endif

向堆中插入节点

堆由 heap_insert 向堆中插入结点。函数将新结点指向调用者传入的数据。首先，要为新的结点重新分配存储空间，以保证树能容纳此结点。新插入的结点将首先放到数组的末尾。此时将破坏堆的固有特性，所以我们必须调整树的结构，对结点进行重新排列。

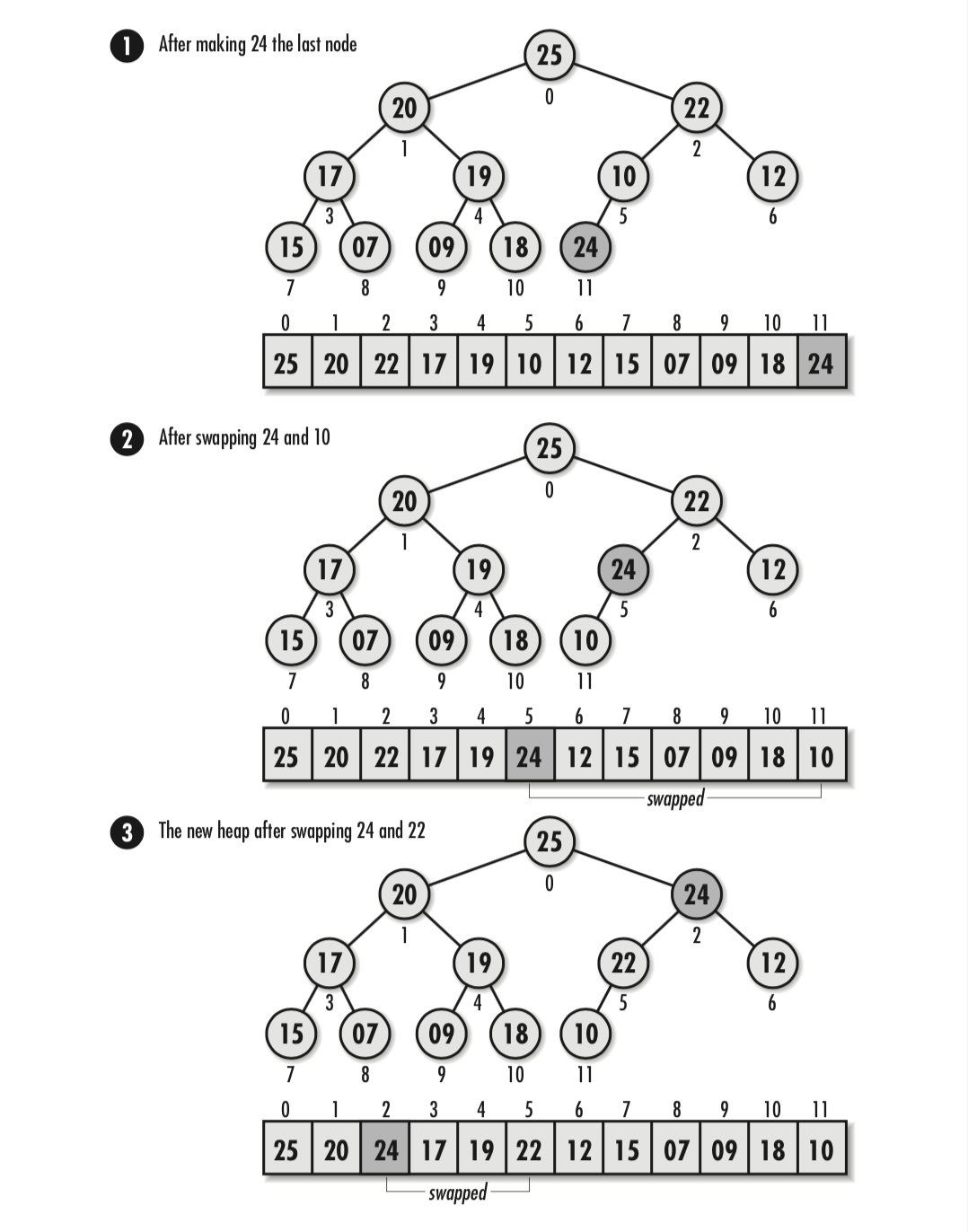
在插入结点时，为了重新排列一棵树，只需要考虑新结点插入的那个分支，因为这是形成堆的局部开始分支。从新结点开始，将结点向树的上方层层移动，比较每个子结点和它的父结点。在每一层上，如果父结点与子结点的位置不正确，就交换结点的内容。这个交换过程会不断进行直到某一层不再需要进行交换为止，或者直到结点到达树的顶部。最后，通过堆数据结构中的 size 成员来更新堆的容量。

heap_insert 的时间复杂度为 O(lgn)，其中n为堆中结点的个数。因为在最坏情况下，需要将新结点中的内容从树的最底层移动到树的顶部，这是一个 lgn 级别的遍历过程。而剩下的操作都能在固定时间内完成。

释放堆顶部节点

堆由 heap_extract 操作来释放堆顶部的结点。首先，将data指向将要释放结点的数据。接下来，保存最后一个结点的内容，将树的大小减一，为树重新分配一个稍小的存储空间。在确定以上操作都成功之后，将最后一个结点中的内容拷贝到根结点中。显然，这个过程会破坏堆固有的特性，所以我们必须调整树的结构，对结点进行重新排列。

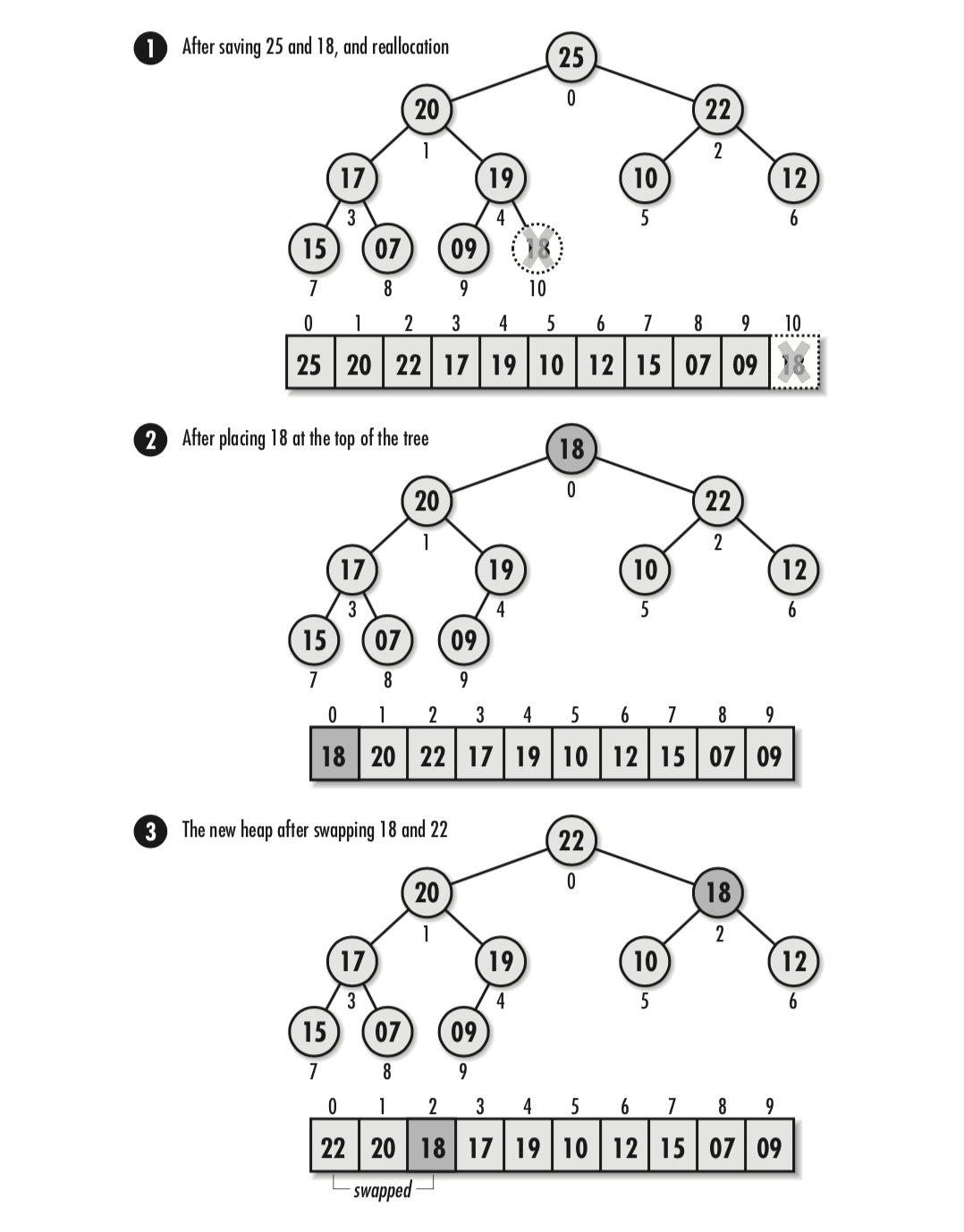
在取出结点后，为了重新排列一棵树，从根结点开始沿树干层层向下移动，与结点的两个子结点进行比较。在每一层上，如果父结点与子结点的位置不正确，就交换结点的内容，此时需要将父结点与位置差异最大的那个子结点进行交换（At each level, if a parent and its children are in the wrong order, we swap their contents and move to the child that was the most out of order）。这个交换过程会不断进行下去直到某一层不再需要进行交换为止，或者直到结点到达一个叶子结点。最后，通过递减堆数据结构中的 size 成员更新堆的容量。

heap_extract的时间复杂度为O(lgn)，其中n为堆中结点的个数。因为在最坏情况下，需要将新结点中的内容从树的顶部移动到树的一个叶子结点，这是一个 lgn 级别的遍历过程。而剩下的操作都能在固定时间内完成。

优先队列

优先队列将数据按照优先级顺序排列。一个优先队列由许多有序的元素构成，所以优先级最高的元素可以有效而快速地确定。例如，我们看一组用来做负载均衡的服务器，时时观察它们的使用情况。当连接请求到达时，优先队列可以告知当前哪个服务器是处理此连接请求的最佳服务器。在这种情况下，最空闲的服务器获取的优先级最高，因为它可以最好地处理服务请求。

优先队列的头文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/*****************************************************************************
*                                                                            *
*  ------------------------------- pqueue.h -------------------------------  *
*                                                                            *
*****************************************************************************/

#ifndef PQUEUE_H
#define PQUEUE_H

#include "heap.h"

/*****************************************************************************
*                                                                            *
*  Implement priority queues as heaps.                                       *
*                                                                            *
*****************************************************************************/

typedef Heap PQueue;

/*****************************************************************************
*                                                                            *
*  --------------------------- Public Interface ---------------------------  *
*                                                                            *
*****************************************************************************/

#define pqueue_init heap_init

#define pqueue_destroy heap_destroy

#define pqueue_insert heap_insert

#define pqueue_extract heap_extract

#define pqueue_peek(pqueue) ((pqueue)->tree == NULL ? NULL : (pqueue)->tree[0])

#define pqueue_size heap_size

#endif

优先队列的示例：包裹分拣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
/*****************************************************************************
*                                                                            *
*  ------------------------------- parcels.c ------------------------------  *
*                                                                            *
*****************************************************************************/

#include <stdlib.h>
#include <string.h>

#include "parcel.h"
#include "parcels.h"
#include "pqueue.h"

/*****************************************************************************
*                                                                            *
*  ------------------------------ get_parcel ------------------------------  *
*                                                                            *
*****************************************************************************/

int get_parcel(PQueue *parcels, Parcel *parcel) {

Parcel             *data;

if (pqueue_size(parcels) == 0)

   /**************************************************************************
   *                                                                         *
   *  Return that there are no parcels.                                      *
   *                                                                         *
   **************************************************************************/

   return -1;

else {

   if (pqueue_extract(parcels, (void **)&data) != 0)

      /***********************************************************************
      *                                                                      *
      *  Return that a parcel could not be retrieved.                        *
      *                                                                      *
      ***********************************************************************/

      return -1;

   else {

      /***********************************************************************
      *                                                                      *
      *  Pass back the highest-priority parcel.                              *
      *                                                                      *
      ***********************************************************************/

      memcpy(parcel, data, sizeof(Parcel));
      free(data);

   }

}

return 0;

}

/*****************************************************************************
*                                                                            *
*  ------------------------------ put_parcel ------------------------------  *
*                                                                            *
*****************************************************************************/

int put_parcel(PQueue *parcels, const Parcel *parcel) {

Parcel             *data;

/*****************************************************************************
*                                                                            *
*  Allocate storage for the parcel.                                          *
*                                                                            *
*****************************************************************************/

if ((data = (Parcel *)malloc(sizeof(Parcel))) == NULL)
   return -1;

/*****************************************************************************
*                                                                            *
*  Insert the parcel into the priority queue.                                *
*                                                                            *
*****************************************************************************/

memcpy(data, parcel, sizeof(Parcel));

if (pqueue_insert(parcels, data) != 0)
   return -1;

return 0;

}